Ba bài toán từ thời cổ Hy Lạp thách đố nhân loại hơn 2500 đã có được giải đáp chính xác năm 2023 nầy do một người Việt tại Vương quốc Anh tìm ra
Cách đây hơn 2500 năm, Toán học bắt đầu phát triển mạnh về Hình học với các nhà toán học lừng danh như Euclide, Hypocrates, Pythagoras, Archimedes và Thales…
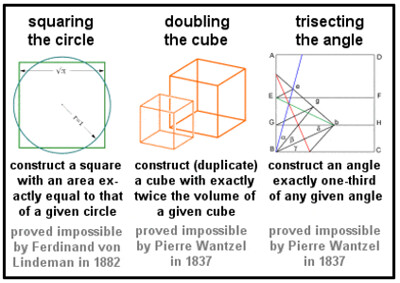
Nhân đôi khối vuông, chia ba một góc và làm vuông hình tròn là những bài toán hình học được đề xuất lần đầu tiên bằng tiếng Hy Lạp cách đây hơn 2500 năm, vốn có ảnh hưởng cực kỳ lớn đến sự phát triển của Hình học. Xưa kia Hy Lạp là quê hương của muôn ngàn những triết gia và nhà khoa học lừng danh. Cách đây hơn 2500 năm, Toán học bắt đầu phát triển mạnh về Hình học với các nhà toán học lừng danh như Euclide, Hypocrates, Pythagoras, Archimedes và Thales…
Toán học Hy Lạp bắt đầu lớn mạnh từ rất sớm, khoảng 700 năm trước Công nguyên, bởi vì triết học Hy Lạp khá phát triển vào thời cổ đại nên mới sản sinh ra Toán học – một môn học vốn phát xuất từ người mẹ đẻ là Triết học. Những nhà toán học Hy Lạp cổ đại thường sống ở các tỉnh thành ven hải phận phía đông Địa Trung Hải. Họ đã để lại nhiều thành quả vĩ đại không thể thay thế cho kho tàng tri thức toán của nhân loại.
Những cống hiến của Hy Lạp cổ đại với toán học, nhìn chung được coi là một trong những cống hiến quan trọng nhất, làm phát triển nhiều phương pháp Toán học và những chủ đề mới của Toán học. Trong số những chủ đề nầy có 3 vấn nạn toán học do Toán học cổ đại Hy Lạp đưa ra thách thức (challenge) nhân loại cách đây hơn 2500 năm và mãi cho đến năm 2022 vẫn chưa có nhà toán học nào phát minh được lời giải đúng. Đó là 3 thách thức Hình học cổ điển rất đơn giản và rất dễ hiểu như sau :
1. Làm vuông hình tròn" (Squaring the Circle),
2. Chia ba một góc (Trisecting an Angle) và
3. Nhân đôi khối vuông (Double the Cube)
với điều kiện giới hạn là "chỉ được dùng thước thẳng (straight edge) và com-pa (compass) để kiến tạo đáp số (construct the answer).
Bất cứ ai học xong Hình học (Geometry) ở bậc trung học đều có thể hiểu 3 đầu đề nói trên, nhưng vì điều kiện giới hạn của 3 bài toán thách thức nầy mà chưa ai giải được nó trong suốt hơn 2 thiên kỷ rưỡi vừa qua.
Mãi cho đến năm nay 2023, một nhà toán học Việt Nam, Trần Đình Sơn, tỵ nạn tại Vương quốc Anh từ năm 1984 đã tìm ra được giải đáp đúng 100% (chứ không phải giải đáp gần đúng) cho 3 thách thức Toán học thiên niên kỷ (millennium challenge) nầy. Ba phát minh vĩ đại nầy đã được các viện quốc tế về Toán công nhận và xuất bản trên Tạp chí Quốc tế về Xu hướng và Công nghệ Toán học (The International Journal of Mathematics Trends and Technology, viết tắt là IJMTT) vào tháng 6, tháng 6 & tháng 8/2023 nầy.
Mặc dù 3 bài toán này có mối liên hệ chặt chẽ với nhau nhưng nhà toán học Việt Nam nói trên đã chọn giải bài toán "Chia ba một góc" (Trisecting an Angle) trước nhất sau khi tình cờ đọc được một ý tưởng (idea) trong Đạo Đức Kinh của triết gia Lão Tử (1) :
"Đại Đạo rất là đơn giản, rất giản dị" !
1. Phát minh thứ nhất (1st Invention) : Chia ba một góc (Tạp chí Toán học Quốc tế/IJMTT số ra ngày 22/5/2023)
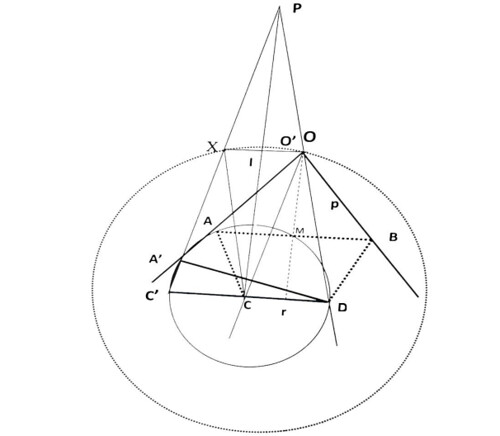
Phép chia ba một góc thành 3 phần bằng nhau là một bài toán cổ điển với yêu cầu chỉ sử dụng hai công cụ : thước thẳng (straightedge không chia độ) và compa. Thật khó để đưa ra ngày tháng chính xác về thời điểm bài toán chia ba góc xuất hiện lần đầu tiên. Tuy nhiên, chúng ta biết rằng Hippocrates, cũng đã nghiên cứu bài toán chia ba một góc, nhưng đã sử dụng một dấu trên thước thẳng để làm cho cây thước không còn là một thước thẳng nữa. Hầu hết các nhà sử học Toán học tin rằng nhiều kết quả đưa ra trong sách Bổ Đề thực sự là do Archimedes và kết quả trên đường xoắn ốc đưa ra về việc chia ba một góc rất phù hợp với tinh thần của tác phẩm. Tuy nhiên, phép chia ba này của Archimedes không phải là một phương pháp chính xác và không sử dụng thước thẳng như đề toán nầy yêu cầu. Phương pháp khác do Nicomedes đưa ra sử dụng đường cong conchoid, nhưng đường cong này không thể vẽ chính xác và mang tính lý thuyết hơn là thực tế. Rõ ràng, cách chia ba góc của Hippocrates, Archimedes hoặc sử dụng conchoid của Nicomedes (khoảng năm 200 trước Công nguyên) là đúng nhưng không tuân theo "luật chơi" tức là sử dụng thước thẳng và compa. Có thể họ đã nghĩ ra đủ mọi cách nhưng không làm được nên phải tự nghĩ ra cách riêng để giải quyết vấn đề này. Về sau, có rất nhiều nỗ lực của các thế hệ nhà Toán học nối tiếp nhau đều không làm được nên họ đã nghĩ ra nhiều cách khác nhau và nhờ đó Toán học có cơ hội phát triển.
Chứng minh cho định lý chia ba một góc
Pierre Wantzel đã chứng minh vào năm 1837 rằng bài toán, như đã nêu, không thể giải được với các góc tùy ý. Năm 1837, Wantzel công bố bằng chứng trên Tạp chí Liouville về "các phương pháp xác định xem một bài toán hình học có thể giải được bằng thước thẳng và compa hay không", và ông là người đầu tiên chứng minh việc chia ba một góc không thể giải được bằng thước thẳng và compa. Nhưng nhà toàn học Việt Nam nầy đã sử dụng thước thẳng và compa để xây dựng đáp số và chứng minh có thể chia ba một góc tùy ý một cách đơn giản mà không cần sử dụng bất kỳ đường cong nào, với công cụ toán học là một số định đề & định lý hình học ở cấp Trung học. Kết quả nầy là một phản chứng (counter-proof) cho phương pháp của Wantzel. Kết quả của phát minh nầy là lời giải chính xác cho thử thách hàng ngàn năm "Chia ba một góc" (Trisecting an Angle) chỉ dùng một thước thẳng, một compa và các định đề & định lý Hình học ờ cấp Trung học Phổ Thông, chứ không hề dùng các phương pháp Toán phức tạp & khó khăn từ cấp Đại học trở lên. Do đó, bất cứ người nào đã học xong Toán Hình học ờ bậc Trung học cũng có thể đọc và hiểu được phát minh nầy.
2. Phát minh thứ hai (2nd Invention) : Làm vuông hình tròn (Tạp chí Toán học Quốc tế/IJMTT số ra ngày 17/06/2023)
Đáp án toán học cho bài toán "Làm vuông hình tròn" (Squaring the Circle) là phát minh thành công thứ hai của nhà toán học Việt Nam nói trên. Lịch sử của bài toán "Làm vuông hình tròn" bằng thước thẳng và compa đã có từ hàng thiên niên kỷ - trước 450 trước Công nguyên (gần 2.500 năm), theo Quanta, một tạp chí khoa học và toán học. Từ xưa cho đến nay, các bài toán liên quan đến số π đã thu hút sự quan tâm của cả giới chuyên môn toán và các nhà toán học không chuyên nghiệp.
"Làm vuông hình tròn" là bài toán tạo dựng một hình vuông có diện tích bằng một hình tròn cho trước bằng cách chỉ sử dụng một số bước hữu hạn với compa và thước thẳng. Trong hình học, kiến tạo (construction) hình bằng "thước thẳng và compa" còn được gọi là kiến tạo Euclide hoặc kiến tạo cổ điển. Nếu hình tròn cho trước có diện tích A thì hình vuông tạo dựng ra phải có cạnh "căn bậc hai" của A & có diện tích bằng A. Nhưng làm sao kiến tạo được hình vuông có cạnh "căn bậc hai" của A một cách chính xác 100% bằng thước thẳng và compa là vấn nạn chưa giải quyết trước năm 2023.
Hippocrates là người đầu tiên sử dụng cách dựng mặt phẳng để tìm một hình vuông có diện tích bằng một hình tròn, nhưng đã thất bại.
Năm 1882, nhà toán học người Đức Ferdinand von Lindemann đã chứng minh rằng Pi (p) là một số vô tỷ (irrational number), nghĩa là không thể dựng được một hình vuông cho bài toán "Làm vuông hình tròn" đã được đề cập bởi Hippocrates. Ông Lindemann đã chứng minh rằng việc "Làm vuông hình tròn" là không thể bằng các công cụ cổ điển !
Bất chấp những chứng minh "không thể" nêu trên bài toán nầy vẫn tiếp tục thu hút trí tưởng tượng của các nhà toán học cũng như công chúng nói chung và nó vẫn là một chủ đề quan trọng trong lịch sử và triết học toán học.
Năm 2023 nhà toán học Việt Nam, Trần Đình Sơn,đã dùng Hình học cấp Trung học giải được bài toán nầy bằng thước thẳng và compa và đã được công nhận và xuất bản trên tạp chí toán quốc tế IJMTT vào tháng 6/2023 (xem trong đường Link/URL nói trên).
3. Phát minh thứ ba (3rd Invention) : Gấp đôi khối vuông (Tạp chí Toán học Quốc tế/IJMTT số ra ngày 29/08/2023)
"Gấp đôi khối vuông" (Double the Cube) là bài toán được mô tả chi tiết như sau : Cho khối vuông có cạnh a và thể tích a³ rồi dùng thước thẳng và compa để tạo dựng một khối vuông có thể tích 2a³.
Trong hình học Euclide cổ điển, người ta đã chứng minh rằng việc "Nhân đôi khối vuông" bằng hai công cụ "thước thẳng & compa" là không thể. Điều không thể xảy ra này bắt nguồn từ thực tế là căn bậc ba của số 2 (cần thiết để nhân đôi khối vuông) không thể tạo dựng (construct) được chỉ bằng thước thẳng và compa. Việc xây dựng yêu cầu tìm độ dài bằng căn bậc ba của số 2, là một số siêu việt. Nhiều nỗ lực khác nhau đã được thực hiện trong suốt lịch sử để giải quyết vấn đề, nhưng chúng liên quan đến các kỹ thuật toán học tiên tiến hơn ngoài các công trình cổ điển. Những phương pháp này thường liên quan đến các khái niệm đại số hoặc hình học vượt ra ngoài phạm vi của cách tạo dựng (construction) hình học bằng thước thẳng và compa truyền thống.
Cho đến năm 2022, không có giải pháp chính xác nào cho thách thức "Nhân đôi khối vuông" chỉ bằng thước thẳng và compa, dựa trên hình học Euclide cổ điển. Công bằng mà nói thì mặc dù bài toán "Làm vuông hình tròn" đã trở nên nổi tiếng nhất ở thời hiện đại, nhưng chắc chắn bài toán "Nhân đôi khối vuông" còn nổi tiếng hơn vào thời Hy Lạp cổ đại.
Thử thách "Nhân đôi khối vuông" yêu cầu một phương pháp xây dựng một khối vuông có thể tích gấp đôi khối vuông đã cho. Điều đó có nghĩa là nếu thể tích khối vuông đã cho là 1 đơn vị thể tích 1 mét khối thì chúng ta phải tạo dựng một khối vuông có cạnh ∛2 từ khối vuông đơn vị đã cho này, chỉ sử dụng compa và thước thẳng. Việc tạo dựng khối vuông có cạnh ∛2 đã từng được cho là không thể thực hiện được theo những hạn chế đã nêu của hình học Euclide.
Lưu ý : Trong hình trên, khối vuông bên trái là khối vuông đã cho đơn vị thể tích là 1 & cạnh đơn vị là 1 ; và khối bên phải là khối vuông nhân đôi có thể tích 2 nhân 13 - 2 & cạnh là căn bậc ba của 2
Bất chấp nỗ lực của nhiều nhà toán học, bài toán này vẫn chưa được giải quyết trong hơn hai nghìn năm và nó trở thành một trong những bài toán chưa giải nổi tiếng và hấp dẫn nhất trong lịch sử toán học. Nó vẫn được nghiên cứu trong các khóa học toán học như một vấn đề mang tính lịch sử và đầy thách thức, đồng thời lời giải của nó tiếp tục truyền cảm hứng và ảnh hưởng đến các nhà toán học cũng như sinh viên.
Nhà toán học người Pháp Pierre Wantzel, 1837, đã chứng minh rằng không thể nhân đôi một khối vuông chỉ bằng thước thẳng và compa. Trong phát minh thứ 3 nầy của nhà toán học Việt Nam nói trên về việc kiến tạo một khối vuông có thể tích gấp đôi một khối vuông cho sẵn, với một độ chính xác 100% đã được chứng minh cũng bằng Hình học ở cấp Trung học và đã được quốc tế thừa nhận và xuất bản cho toàn cầu vào tháng 8/2023 vừa qua. Các kết quả thu được có thể kết luận rằng tuyên bố về tính không thể của Wantzel không có giá trị về mặt hình học, vì nó không đưa ra mối quan hệ hình học giữa bậc hai và phần mở rộng bậc ba. Nhà toán học Việt Nam nầy đã tuân thủ nghiêm ngặt các ràng buộc trong việc sử dụng thước thẳng và compa để phát triển một phương pháp giải chính xác bài toán "Nhân đôi khối vuông" bằng hình học theo một kỹ thuật đặc biệt.
Tóm lại, những bài toán thách thức cổ điển này cực kỳ quan trọng trong sự phát triển của hình học. Ba bài toán như vậy đã thu hút rất nhiều sự quan tâm của các nhà hình học sau này đến nỗi chúng được gọi là những "bài toán cổ điển" vĩ đại : "Chia ba một góc" (Trisecting an Angle), "Làm vuông hình tròn" (Squaring the Circle) và "Nhân đôi khối vuông" (Double the Cube". Giờ đây vào năm 2023 nầy chúng đã được giải quyết chính xác bời một người Việt tỵ nạn thuộc thế hệ thứ nhất tại Vương quốc Anh và phát minh nầy đã được quốc tế thừa nhận & xuất bản như một phát minh Toán rất vĩ đại của thế kỷ 21.
Đan Tâm
(25/09/2023)
(1) Lao Tzu (Author of Tao Te Ching) : "The great Tao is very simple, very simple !" (Lão Tử -tác giả của Đạo Đức Kinh : "Đại Đạo rất là đơn giản, rất giản dị")